数学运算常用解题技巧——特殊值法、方程法、图解法、整体法和极端法等。
技巧一 特殊值法
特殊值法,就是在题目所给的范围内取一个恰当的特殊值直接代入。常应用于和差倍比问题、行程问题、工程问题、浓度问题、利润问题、几何问题等。
【例题1】
单独完成某项工作,甲需要16小时,乙需要12小时,如果按照甲、乙、甲、乙、……的顺序轮流工作,每次1小时,那么完成这项工作需要多长时间?
A.13小时40分钟 B.13小时45分钟
C.13小时50分钟 D.14小时

技巧二 方程法
方程法是指将题目中未知的数用变量(如x,y)表示,根据题目中所含的等量关系,列出含有未知数的等式(组),通过求解未知数的数值,来解应用题的方法。因其为正向思维,思路简单,故不需要复杂的分析过程。
解题步骤:设未知量——找等量关系——列方程(组)——解方程(组)。
方程法应用较为广泛,适用于绝大部分题目,如行程问题、工程问题、盈亏问题、和差倍比问题、浓度问题、利润问题、年龄问题等均可以通过方程法来求解。
【例题2】

技巧三 图解法
图解法是指利用图形来解决数学运算的方法,将复杂的数字之间的关系用图形形象地表示出来。包括线段图、网状图/树状图、文氏图和表格。图解法适用于绝大部分题型,尤其是在行程问题、年龄问题、容斥问题等强调分析过程的题型中运用得很广。
【例题3】
甲从某地出发匀速前进,一段时间后,乙从同一地点以同样的速度同向前进,在K时刻乙距起点30米;他们继续前进,当乙走到甲在K时刻的位置时,甲离起点108米。此时乙离起点( )。
A.39米 B.69米 C.78米 D.138米
【解析】此题答案为B。在解行程问题时,通常先画出线段图,这样可以直观清晰地看到状态变化的过程和各个量之间的关系,帮助我们准确求解。
根据题意可画出下图:
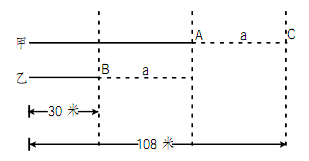
如图所示,在K时刻,甲和乙分别在A、B两点,且相隔距离为a,他们继续前进,由题意乙从B点前进到A点,同时甲从A点前进到C点,两人以相同的速度匀速前进,那么A、C两点之间的距离也为a,则a=(108-30)÷2=39米,即甲、乙之间的距离为39米,故此时乙离起点30+39=69米。
技巧四 极端法
极端法是指通过考虑问题的极端状态,探求解题方向或转化途径的一种常用方法。极端法一般适用于鸡兔同笼问题、对策分析类问题等。
运用极端法的情况主要有分析极端状态和考虑极限图形与极限位置两种情况。
1.分析极端状态:先分析并找出问题的极限状态,再与题干条件相比较,作出相应调整,得出所求问题的解。
2.考虑极限图形与极限位置:
(1)极限图形,主要是利用一些几何知识。
(2)极限位置,首先找到途中满足条件的极端位置,再判断极端位置与题中所求之间的关系,进而求出题目答案。
【例题4】
10个箱子总重100公斤,且重量排在前三位的箱子总重不超过重量排在后三位的箱子总重的1.5倍。问最重的箱子重量最多是多少公斤?


